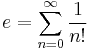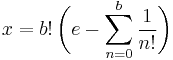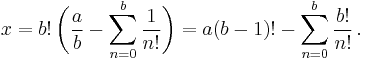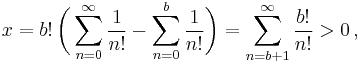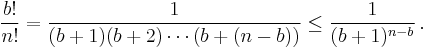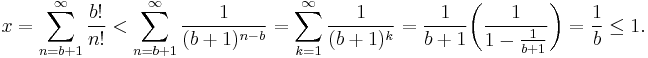Proof that e is irrational

Part of a series of articles on
The mathematical constant $e$

Natural logarithm · Exponential function

Applications in: compound interest · Euler's identity & Euler's formula · half-lives & exponential growth/decay

Defining $e$ : proof that $e$ is irrational · representations of $e$ · Lindemann–Weierstrass theorem

In mathematics, the series representation of Euler's number e

$e = \sum_{n = 0}^{\infty} \frac{1}{n!}\!$

can be used to prove that e is irrational. Of the many representations of e, this is the Taylor series for the exponential function e^y evaluated at y = 1.

1 Summary of the proof
2 Proof
3 See also
4 References

Summary of the proof

This is Joseph Fourier's proof by contradiction. Initially e is assumed to be a rational number of the form a/b. We then analyze a blown-up difference x of the series representing e and its strictly smaller b^th partial sum, which approximates the limiting value e. By choosing the magnifying factor to be the factorial of b, the fraction a/b and the b^th partial sum are turned into integers, hence x must be a positive integer. However, the fast convergence of the series representation implies that the magnified approximation error x is still strictly smaller than 1. From this contradiction we deduce that e is irrational.

Proof

Towards a contradiction, suppose that e is a rational number. Then there exist positive integers a and b such that e = a/b.

Define the number

$x = b!\,\biggl(e - \sum_{n = 0}^{b} \frac{1}{n!}\biggr)\!$

To see that if e is rational, then x is an integer, substitute e = a/b into this definition to obtain

$x = b!\,\biggl(\frac{a}{b} - \sum_{n = 0}^{b} \frac{1}{n!}\biggr) = a(b - 1)! - \sum_{n = 0}^{b} \frac{b!}{n!}\,.$

The first term is an integer, and every fraction in the sum is actually an integer because n ≤ b for each term. Therefore x is an integer.

We now prove that 0 < x < 1. First, to prove that x is strictly positive, we insert the above series representation of e into the definition of x and obtain

$x = b!\,\biggl(\sum_{n = 0}^{\infty} \frac{1}{n!} - \sum_{n = 0}^{b} \frac{1}{n!}\biggr) = \sum_{n = b%2B1}^{\infty} \frac{b!}{n!}>0\,,\!$

because all the terms with n ≤ b cancel and the remaining ones are strictly positive.

We now prove that x < 1. For all terms with n ≥ b + 1 we have the upper estimate

$\frac{b!}{n!} =\frac1{(b%2B1)(b%2B2)\cdots(b%2B(n-b))} \le\frac1{(b%2B1)^{n-b}}\,.\!$

This inequality is strict for every n ≥ b + 2. Changing the index of summation to k = n – b and using the formula for the infinite geometric series, we obtain

$x =\sum_{n = b%2B1}^\infty \frac{b!}{n!} < \sum_{n=b%2B1}^\infty \frac1{(b%2B1)^{n-b}} =\sum_{k=1}^\infty \frac1{(b%2B1)^k} =\frac{1}{b%2B1} \biggl(\frac1{1-\frac1{b%2B1}}\biggr) = \frac{1}{b} \le 1.$

Since there is no integer strictly between 0 and 1, we have reached a contradiction, and so e must be irrational. Q.E.D.

The above proof can be found in Proofs from THE BOOK, where the stronger result that e^q is irrational for any non-zero rational q is also proved.^[1]

References

^ Aigner, Martin; Ziegler, Günter M. (1998), Proofs from THE BOOK, Berlin, New York: Springer-Verlag, pp. 27–36 .

Proof that e is irrational

Contents

Summary of the proof

Proof

See also

References